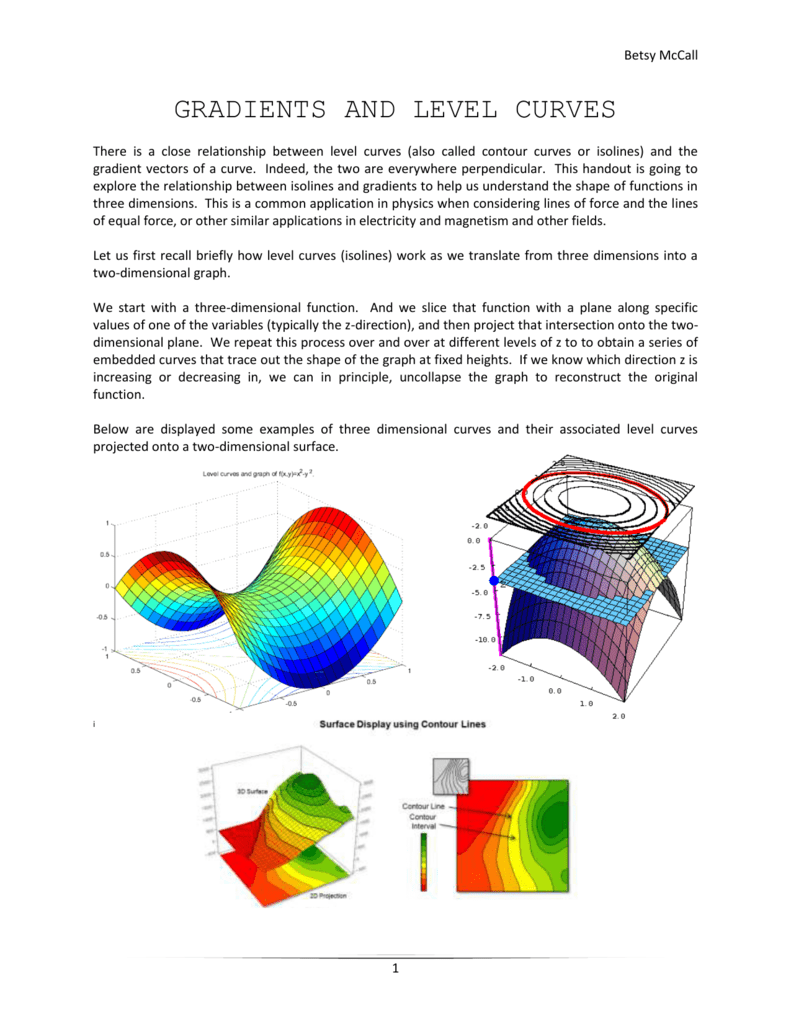
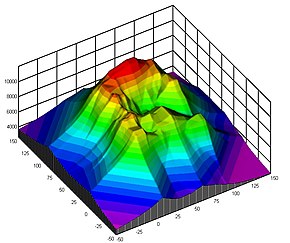
2/2/ How To Create contour lines in ArcGIS Pro Summary Contour lines help visualize surface topology by creating line connecting points with an equal elevation above or below a standard level This is useful in identifying suitable locations for projects, such as estimating water storage capacity, or approximating the volume of excavation workLevel curves of G (x, y) are shown in the figure below Find its approximate x and yderivatives at (3, 3) Ans {10/13, 10/14} 3 Let the figure below be the contour diagram of f (x,y ) Find an approximate x derivative at (2, 2) eg 8 Find a formula for the slopes of the tangent lines to a curve cut from the elliptic paraboloidThere is a close relationship between level curves (also called contour curves or isolines) and the gradient vectors of a curve Indeed, the two are everywhere perpendicular This handout is going to explore the relationship between isolines and gradients to help us understand the shape of functions in three dimensions This is a common application in physics when considering lines of force and the lines

Level Curves Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
Level curves function contour lines
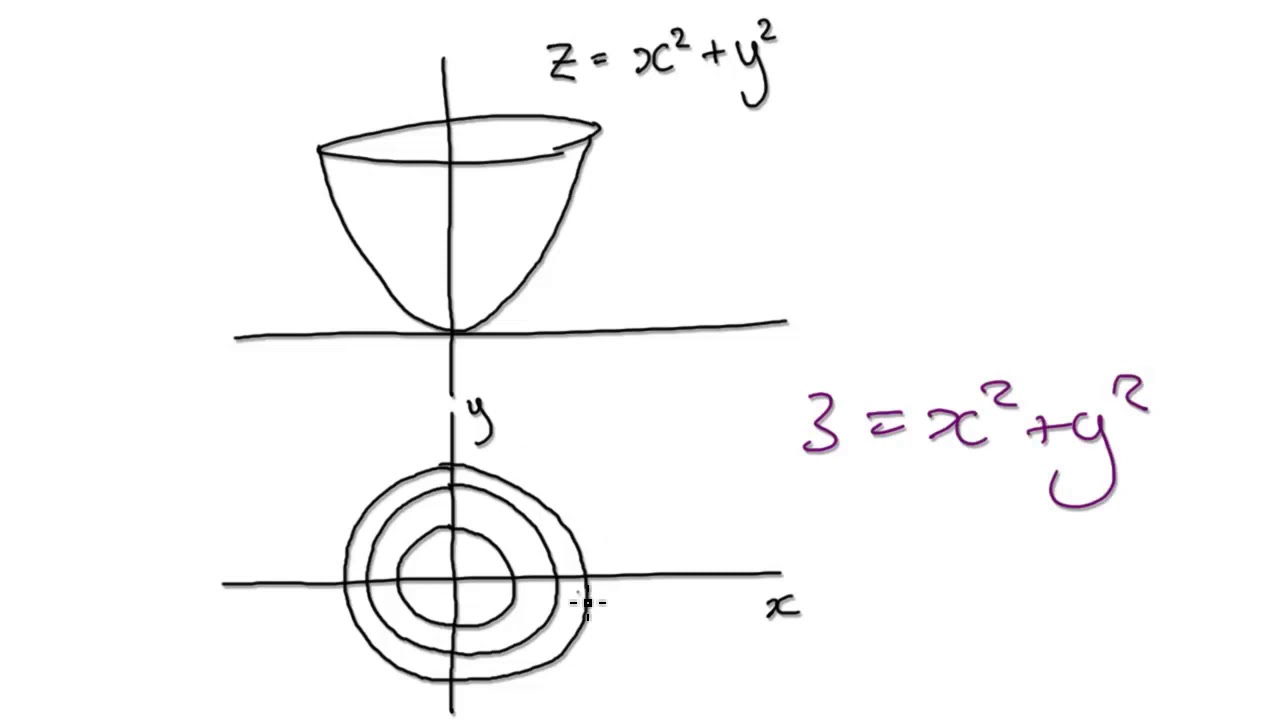
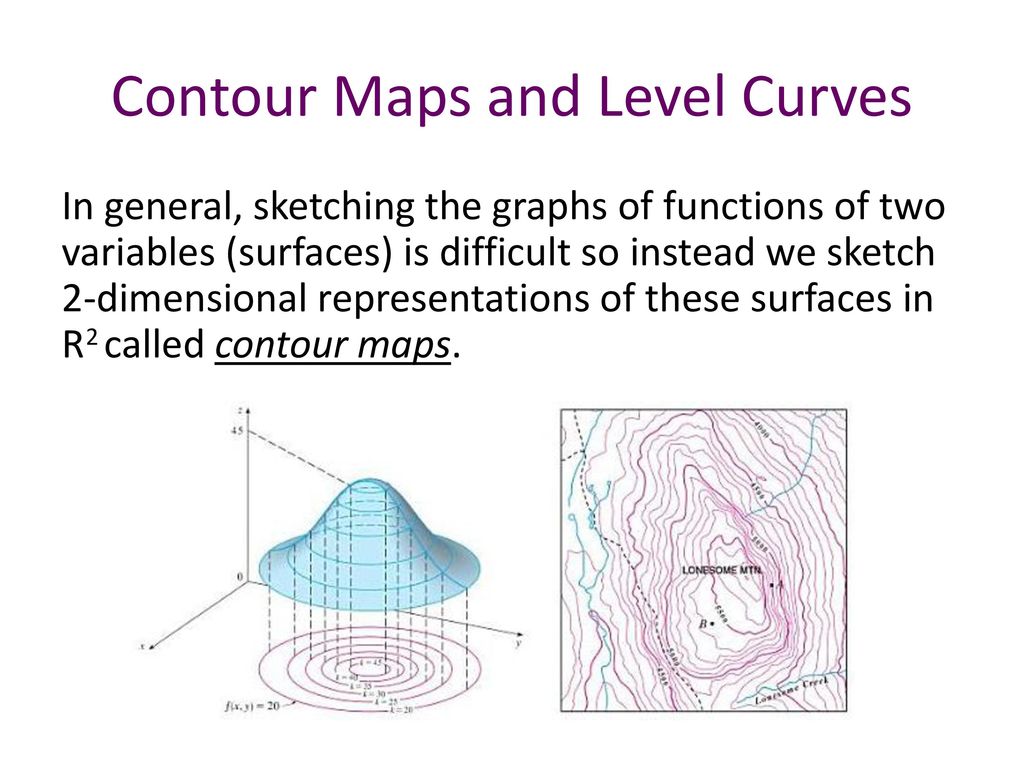
Level curves function contour lines-A graph of (some of) the level curves of a function is called a contour plot (it looks like a topographical map) Example Let's plot of the surface and several horizontal planes The curves of intersection are level curves (or contours) at levels and 1An Aframe level is a simple tool that allows us to easily find contours on the land, enabling us to build garden beds that harvest17/6/21 Calc 3 Level curves Close 1 Posted by 6 years ago Archived Calc 3 Level curves Let k(x,y)= 4x 2 8x 5y 2 3 Sketch the level curves for c= 1, 15, and I got a hyperbola from this, but now I'm in doubt because one of the values of c make it undefined Is this possible?When drawing in three dimensions is inconvenient, a contour map is a useful alternative for representing



Functions Of Several Variables Ximera
You can change which values the contour lines should display by tweaking the "Range of contour levels" and "Number of contour levels" sliders By default they are set to (100,100) and 21 respectively, so this means that the displayed contour levels will start at 100 and go up to and including 100 in intervals of» Clip Level Curves and Contour Plots () From Lecture 8 of 1802 Multivariable Calculus, Fall 07 Flash and JavaScript are required for this featureLevel Curves The level curves are curves of constant elevation above sea level If you walk along one of these contour lines, you neither ascend nor descend Another common example is the temperature function introduced in the opening paragraph of this section Here the level curves are called isothermals and join locations with the same
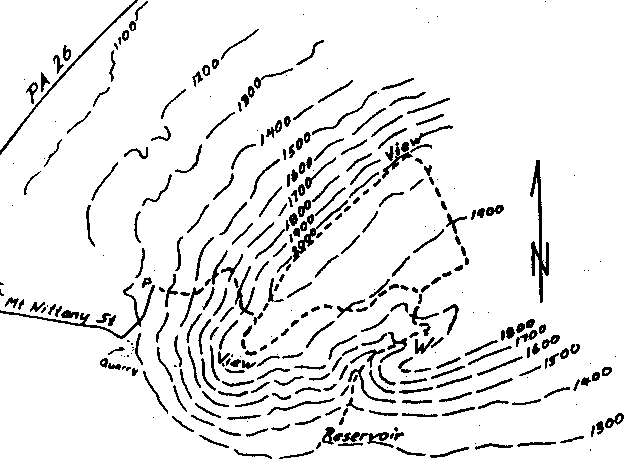
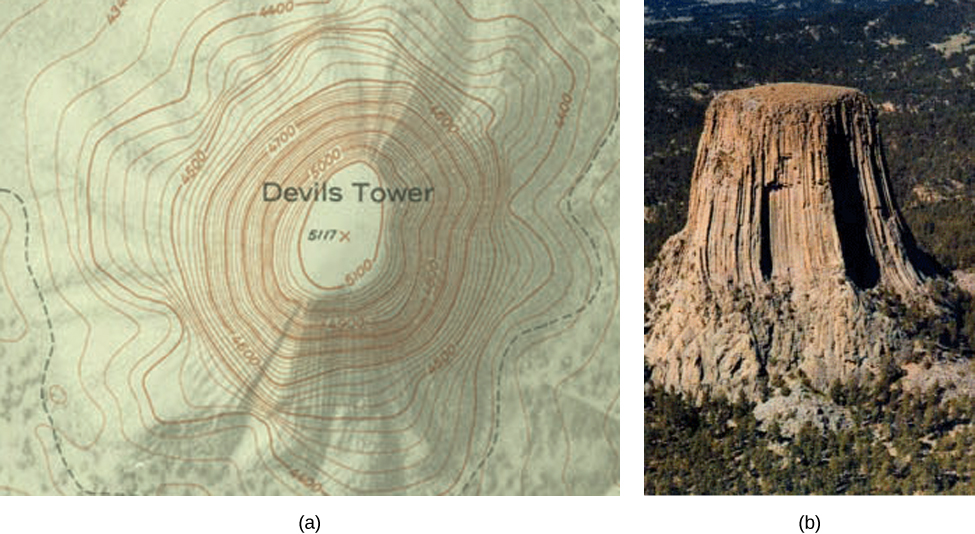
Based on the syllabus Fifth Semester MAT5 B05 Mathematics Vector Calculus (UNIVERSITY OF CALICUT) In this session we describe level curves and contour lNew url for the 3D plotter https//wwwmonroeccedu/faculty/paulseeburger/calcnsf/CalcPlot3D/This video explains how to graph contour plots for functions oOne common example of level curves occurs in topographic maps of mountainous regions, such as the map in Figure 2 The level curves are curves of constant elevation of the Gran canyon Notice that if you walk along one of these contour lines you neither ascend nor descend Figure 2 Gran Canyon topographic map
Visit wwweconomicswithfranciscocom (English) wwweconomiaycienciacom (Spanish)Level Curves or Contour Curves that will help to undersAny markers defined by style are ignored4 Create contour lines For this, we select CivilCAD> Altimetry> Contour lines> Terrain In the panel that appears we configure every few meters we want the main and secondary level curves;




Level Set Examples Math Insight



Contour Plot Under Surface Plot Matlab Surfc
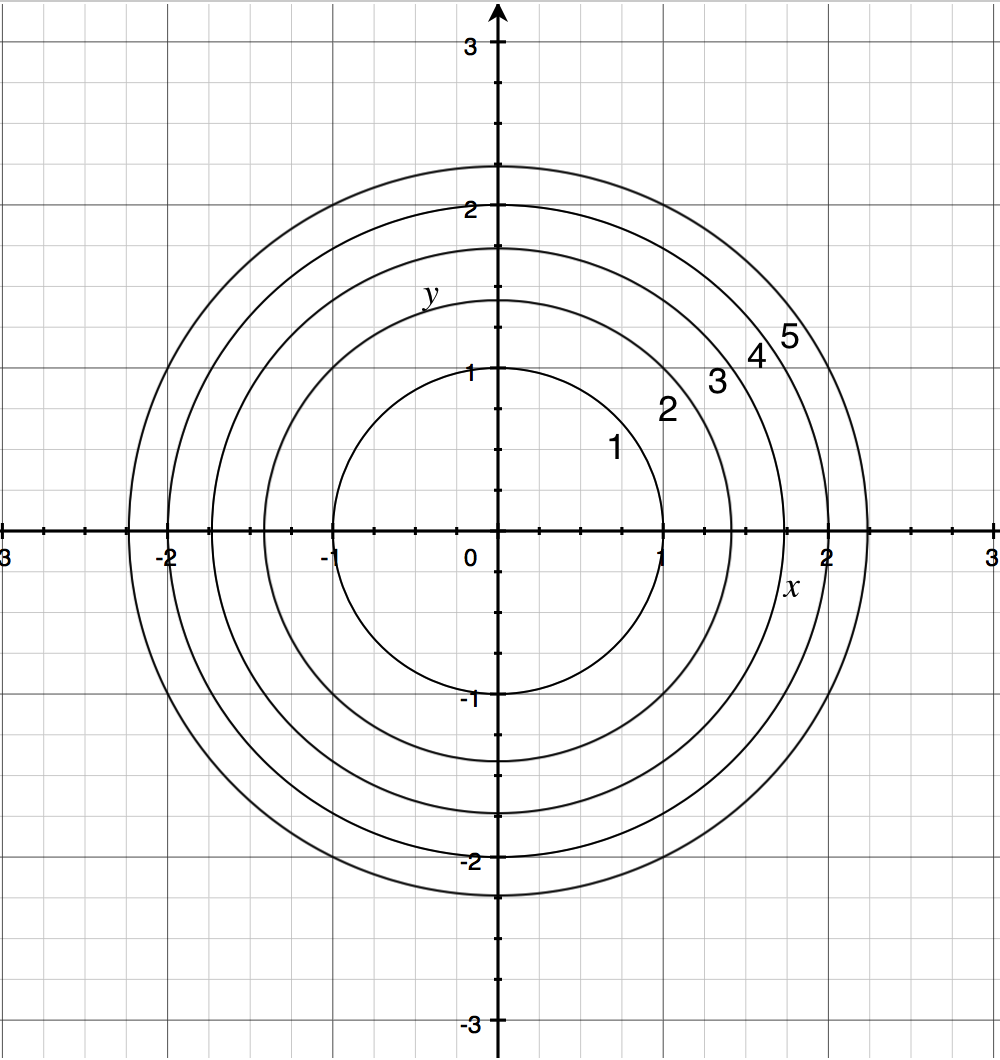
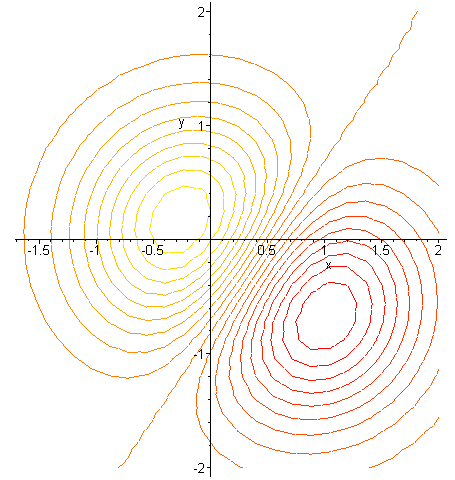
7/6/21 1 27 27 2k ?Ie the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below isLevel curves are always graphed in the x yplane, x yplane, but as their name implies, vertical traces are graphed in the x z x z or y zplanes y zplanes Definition Consider a function z = f ( x , y ) z = f ( x , y ) withLevel curves The two main ways to visualize functions of two variables is via graphs and level curves Both were introduced in an earlier learning module Level curves for a function z = f ( x, y) D ⊆ R 2 → R the level curve of value c is the curve C in D ⊆ R 2 on which f C = c Notice the critical difference between a level curve CAsk Question Asked 6 years, 2 months ago Active 6 years, 2 months ago Viewed 548 times But I don't quite know how to use this knowledge to sketch the level curves of f calculus Share Cite Follow edited Jun 1




Contour Plots Video Khan Academy



1
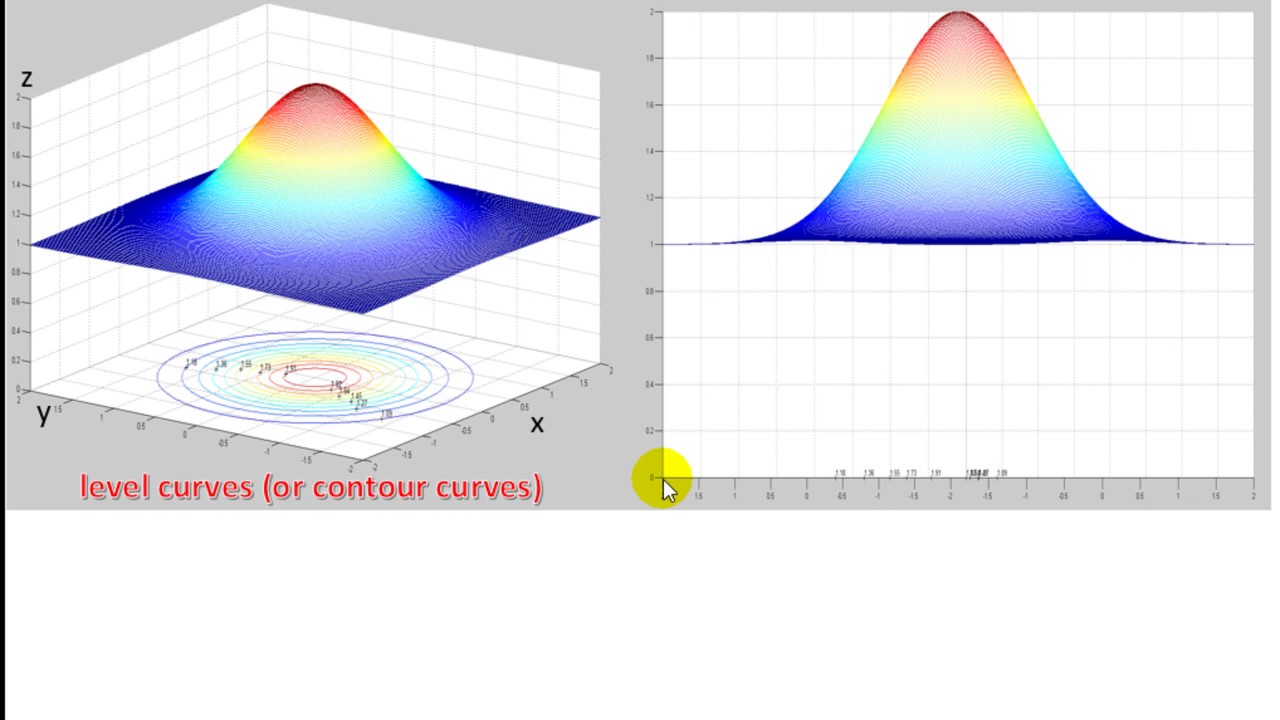
Ie the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below is the surface Examine the level curves of the functionPlot level curves (contour lines) of the matrix z, using the contour matrix c computed by contourc from the same arguments;Contour plot is a collection of contour lines Each contour is a curve that is a resultant of cutting a surface by a plane Every contour need not form a curve Some of the resultant contours can be a straight line as well Here is the formal definition of a contour plot A level curve of a function f (x,y) is the curve of points (x,y) where f




Introduction To Functions Of Several Variables Ppt Download




Level Curves Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
1/6/15 Sketch the level curves (contour lines) of the function?Lecture Notes (Chapter 11 part2_ContourLines, Level Curves and 3D Graphs)pdf Free download as PDF File (pdf), Text File (txt) or read online for free6/5/16 If you're working with some other 3D graph then, you'll want to check to find which values of x and y together produce z The easiest way to do this is to set a fixed value for one variable and then solve for the other So, if you have a function F (x,y) = 2x 3y, and you want to create a contour line for z = 3




Draw A Contour Map Of The Function Showing Several Level Curves F X Y Y X 2 Y 2 Youtube



Level Curves And Contour Plots Mathonline
Often a thicker line is used for every Imagine that the 3d surface is sliced with horizontal planes every and then the lines where the surface and the plane intersect are projected down into the xy plane Important Level curves are in the xy plane One level curve consists eg of all (x,y) points which satisfy f(x,y)=10013/8/21 Plot contour lines Call signature contour( X, Y, Z, levels, **kwargs) contour and contourf draw contour lines and filled contours, respectively Except as noted, function signatures and return values are the same for both versions Parameters X, Yarraylike, optional The coordinates of the values in ZContour lines from Google Earth in 3 steps This article explains how to generate contour lines from the Google Earth digital model For this we will use a plugin for AutoCAD Step 1 Display the area where we want to obtain the Google Earth digital model Step 2 Import the digital model Using AutoCAD, having the PlexEarth Addins installed



Gradients Level Curves




Functions Of Several Variables Ximera
Partial Derivatives, Gradients, and Plotting Level Curves Here we will explore how to compute partial derivatives and gradients in Maple (and thus find linearizations of functions) We will also look at plotting level curves (contours), level surfaces, gradient vectors, tangent planes and normal lines Maple worksheet contoursmwContour curve a 3D curve formed by the intersection of a 3D surface and a plane f(x;y)=z=k, where k is a constant value level curve the projection of a contour curve onto the x;y plane Common uses of level curves are to show elevations above sealevel in topographic maps and to show atmospheric pressure in isobaric maps Figure 1a is anLecture Notes (Chapter 11 part2_ContourLines, Level Curves and 3D Graphs)pdf Free download as PDF File (pdf), Text File (txt) or read online for free math 3



Describe The Level Curves Of The Function Z 12 4x Chegg Com




Level Sets Math Insight
LEVEL CURVES The level curves (or contour lines) of a surface are paths along which the values of z = f(x,y) are constant;15/9/ A contour line is a curve that joins points of equal value In cartography, contour lines join the points of equal elevation above a given standard level like the mean sea level A contour map is a map to illustrate the topographical features of an area using contour lines It is often used to show the heights, slopes and depths of valleys andBoth contourplot and contourplot3d take the same arguments and generate a contour plot for a given expression or function In other words, these commands both produce a set of level curves of the input function for a discrete set of values (ie levels) of the third coordinate



Level Curves And Contour Plots




Find And Sketch The Level Curves F X Y C On The Same Set Of Coordinates Axes For The Given Values Of Brainly Com
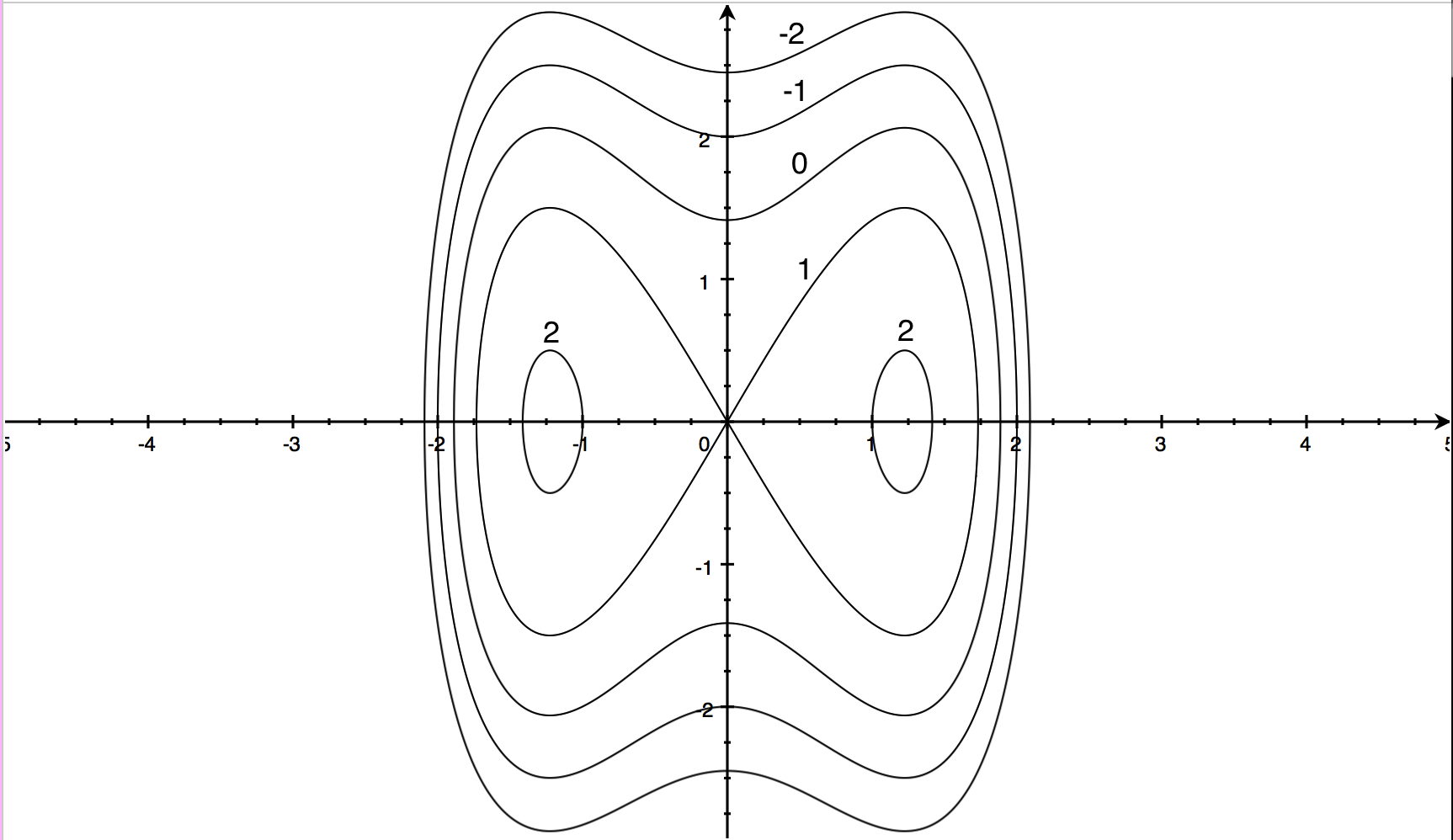
We begin the new topic on Level Curves & Contour lines Their difference and their relationContourPlot by default generates colorized grayscale output, in which larger values are shown lighter At positions where f does not evaluate to a real number, holes are left so that the background to the contour plot shows through ContourPlot treats the variables x and y as local, effectively using BlockA contour line (also isoline, isopleth, or isarithm) of a function of two variables is a curve along which the function has a constant value, so that the curve joins points of equal value It is a plane section of the threedimensional graph of the function (,) parallel to the (,)planeMore generally, a contour line for a function of two variables is a curve connecting points where the




Level Curves Of Functions Of Two Variables Youtube



Video3144 Calculus 3 Introduction To Level Curves Youtube
See how interesting the feedback that should have had the boys of ArqCOM, when people suggested that they were called Thin Curves and Thick CurvesLevel Curves and Critical Points Course Home Syllabus Now, notice that both of these that I've drawn, if we don't label the contour lines, these have the same contour plot, because the concentric rings on C, which are telling us that the function in increasing, they're the same below, because this is essentially the same thingKeep in mind at any given point (x, y), there are infinite directions we could move Each affects f (x, y) differently Just two directions don't affect it at all those are the contour line directions When we move perpendicularly to the contour line, that direction changes f (x, y)



Contour Maps Article Khan Academy




Cal123 Level Curves And Contour Diagrams Pdf Contour Line Curve
Level sets show up in many applications, often under different names For example, an implicit curve is a level curve, which is considered independently of its neighbor curves, emphasizing that such a curve is defined by an implicit equationAnalogously, a level surface is sometimes called an implicit surface or an isosurface The name isocontour is also used, which means a contour of16/9/ Contour lines are imaginary lines that connect places at the same height above sea level These are recorded in brown on the survey maps These documents appear to be closed curves The height difference between the two adjacent contour lines on the survey map is mIf None is passed (or the option is not given), then the number of contour lines is determined automatically, and is usually about 5 linewidths – integer or list of integer (default None), if a single integer all levels will be of the width given, otherwise the levels




Describe The Level Curves Of The Function Z X Y Chegg Com




Contour Maps In Matlab
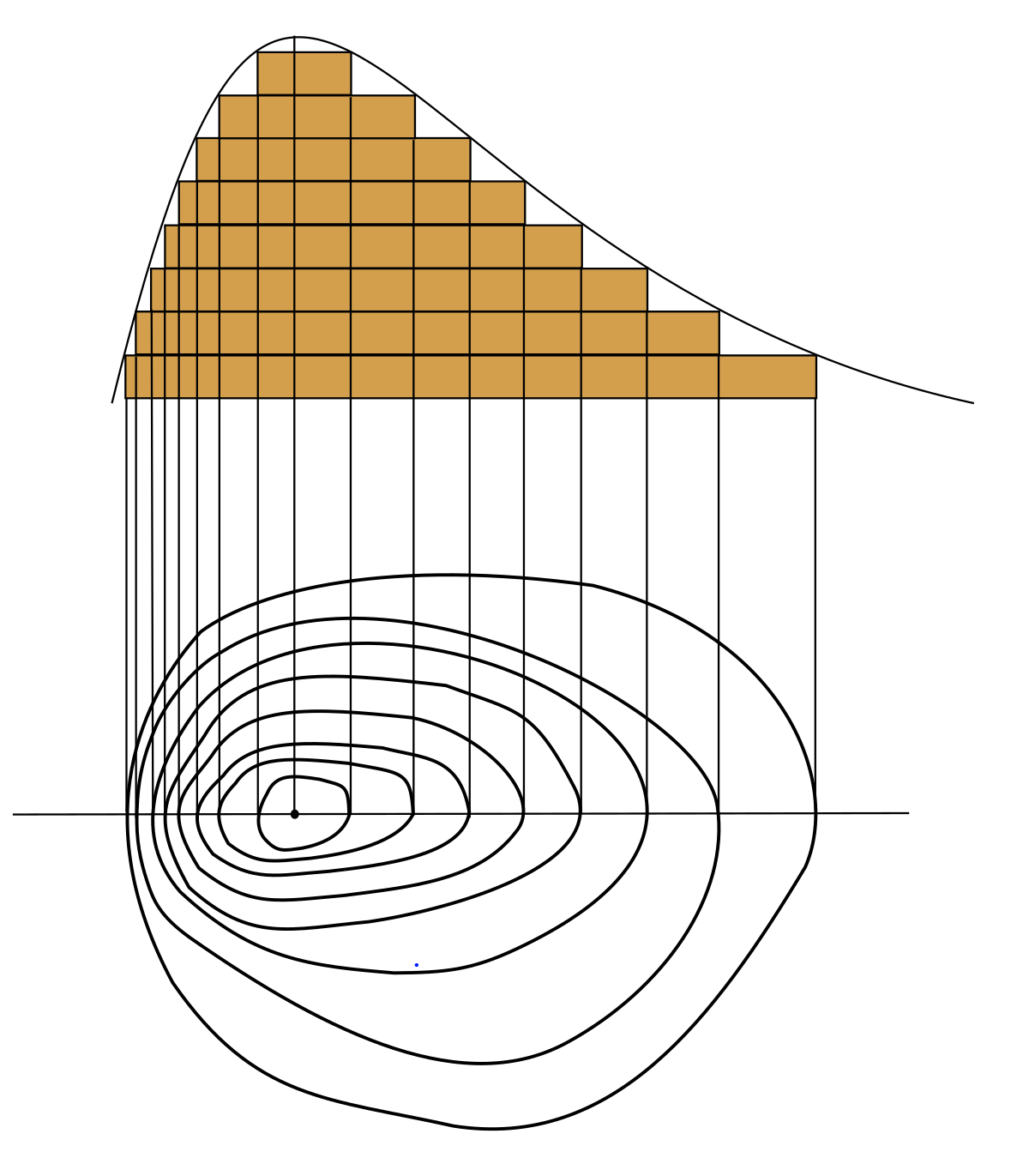
18/6/21 One common example of level curves occurs in topographic maps of mountainous regions, such as the map in Figure 2 The level curves are curves of constant elevation Notice that if you walk along one of these contour lines you neither ascend nor descend FigureLevel curves are in the xy plane One level curve consists eg of all (x,y) points which satisfy f(x,y)=100 If , then this level curveLevel Curves and Contour Plots Level curves and contour plots are another way of visualizing functions of two variables If you have seen a topographic map then you have seen a contour plot Example To illustrate this we first draw the graph of z = x2 y2 On this graph we draw contours, which are curves at a fixed height z = constantGraphs of Surfaces and Contour Diagrams 3 Together they usually constitute a curve or a set of curves called the contour or level curve for that value In principle, there is a contour through every point In practice, just a few of them are shown The following is the contour diagram for the earlier surface 0 0 0 0 0 0 0 2 2




Sketching A Contour Map In Describe The Level Chegg Com
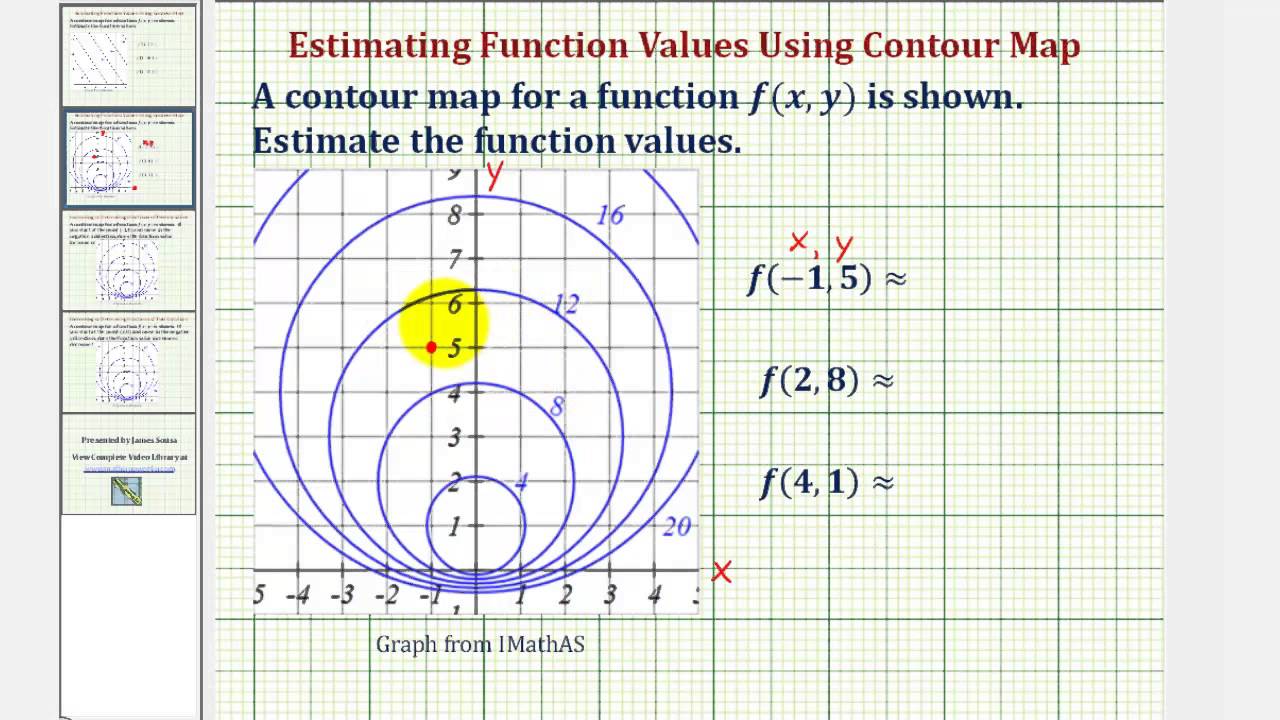



Ex 2 Determine A Function Value Using A Contour Map Youtube
50 level curves and contour lines Difference between level curves and contour lines Direct link to Kunal Muley's post "At 241 in the video we see that the contour lines" in the video we see that the contour lines for z=1, not intersecting at point (0,0)26/5/ You've probably seen level curves (or contour curves, whatever you want to call them) before If you've ever seen the elevation map for a piece of land, this is nothing more than the contour curves for the function that gives the elevation of the land in that area Of course, we probably don't have the function that gives the elevationLearn all about level curves Get detailed, expert explanations on level curves that can improve your comprehension and help with homework



Surfaces Part 6




Calculus Iii Functions Of Several Variables
22/5/21 Level Curves For twovariable functions, is usual to use contour lines called level curves If a function is given by the expression z=f(x,y) and we make f(x,y)= c, this equation corresponds toThe level curves (or contour lines) of a surface are paths along which the values of z = f (x,y) are constant;Level curves level curves Log InorSign Up x 2 y 2 − z 2 = 1 1 z =See the latter for their interpretation The appearance of contour lines can be defined with a line style style in the same manner as plot Only line style and color are used;



Contours



0 3 Visualizing Functions Of Several Variables



Contour Line Wikipedia



Announcements Topics To Do Ppt Download



Surfaces Part 6



Www Arnoldfw Com Pdf Contour Plots Pdf



Contour Maps Article Khan Academy



Surfaces Part 6




Level Curves




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware




Locus Of Osculation For Two Families Of Ellipsoidal Level Curves Download Scientific Diagram



14 Partial Derivatives Ppt Download



Contour Maps Article Khan Academy



1



1



Level Curves And Contour Plots Mathonline




14 8 Lagrange Multipliers Mathematics Libretexts
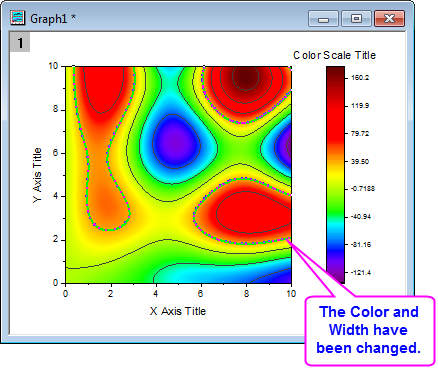



Help Online Tutorials Contour Plots And Color Mapping




Describe The Level Curves Of The Function Z X2 Chegg Com



Level Curves And Contour Plots Mathonline



Level Curves Or Contour Curves Youtube




Lagrange Multipliers
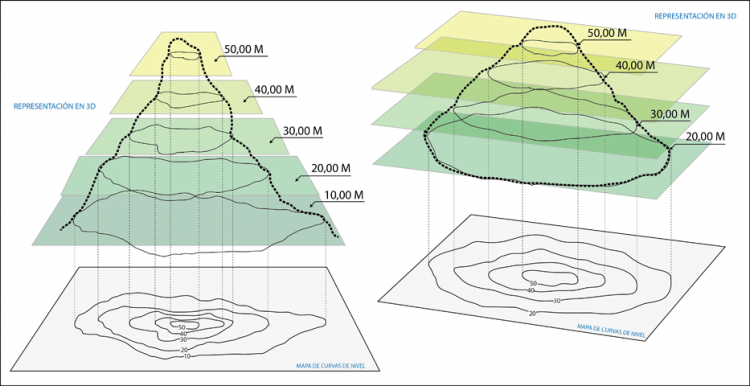



Building Elevation And Topographical Maps Using Deep Learning




Contour Maps Article Khan Academy



Contour Lines Rodolphe Vaillant S Homepage




Contour Maps In Matlab
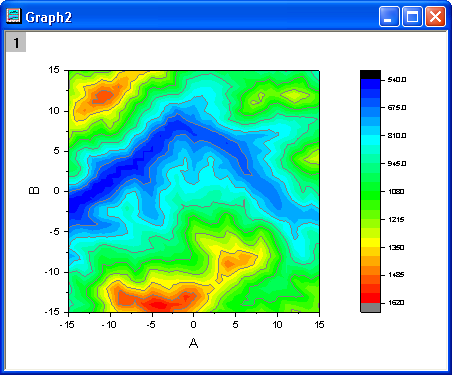



Help Online Tutorials Contour Plots And Color Mapping




Calculus Iii Functions Of Several Variables




Level Curves Contours Of Arrokoth Topographic The Color Bar Denotes Download Scientific Diagram




Level Curves




13 1 Day 2 Level Curves Level Curves One Way To Visualize A Function Of Two Variables Is To Use A Scalar Field In Which The Scalar Z F X Y Is Assigned




11 Level Curves And Contour Lines Of Functions Of Two Variables Youtube




Level Curves
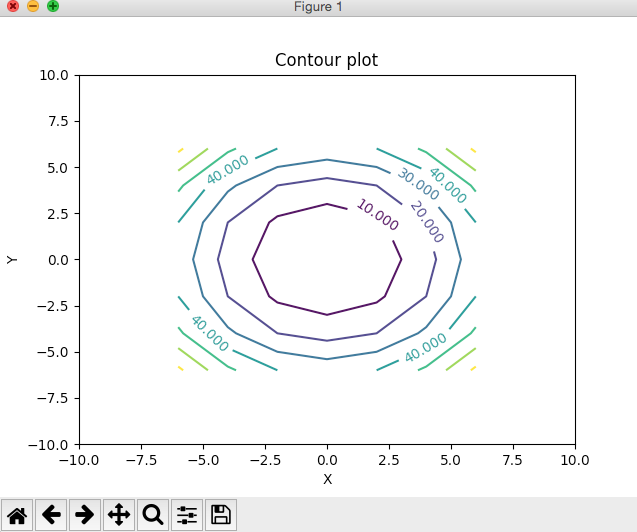



Contour Plot Using Python And Matplotlib Pythontic Com
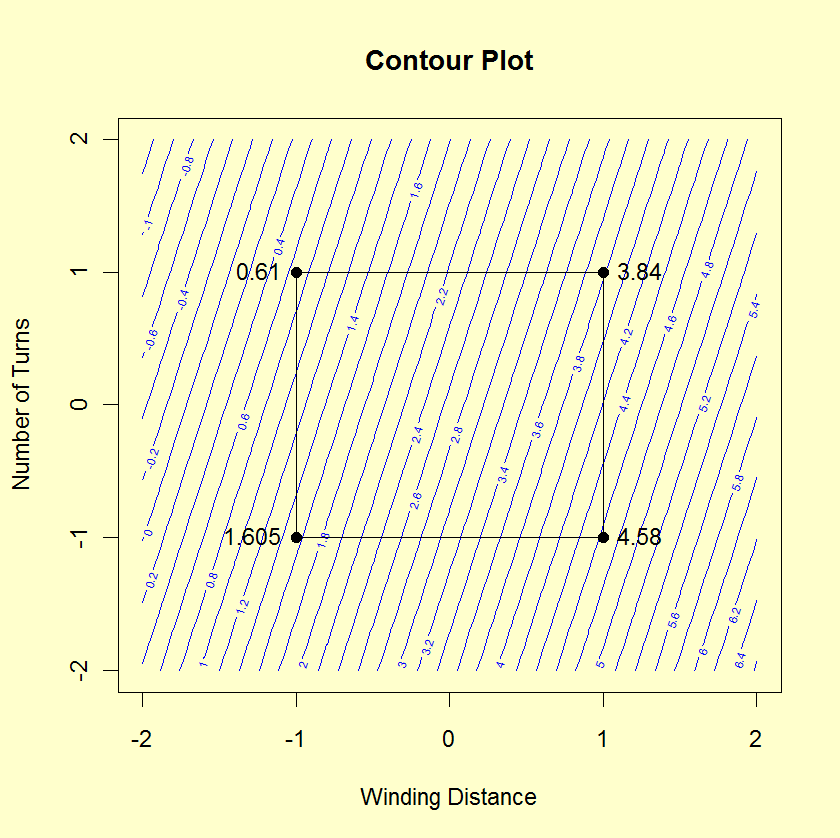



1 3 3 10 1 Doe Contour Plot




Level Curves



Level Curves And Contour Plots Mathonline




Function Reference Contour




Level Curves For The Region Of The Potential Energy Surface With The Download Scientific Diagram
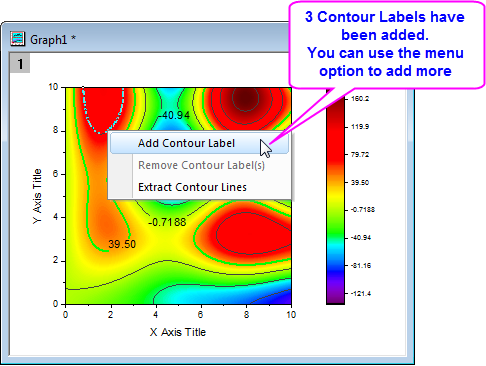



Help Online Tutorials Contour Plots And Color Mapping




Level Set Wikipedia




Maple Tutor Part 11




How To Sketch Level Curves Youtube



Contour Lines Rodolphe Vaillant S Homepage



Contour Lines Rodolphe Vaillant S Homepage
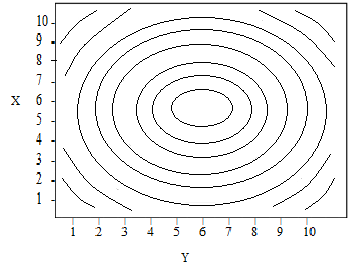



Contour Plots Definition Examples Statistics How To



1




Matlab Tutorial




Calculus Iii Functions Of Several Variables




Functions Of Several Variables
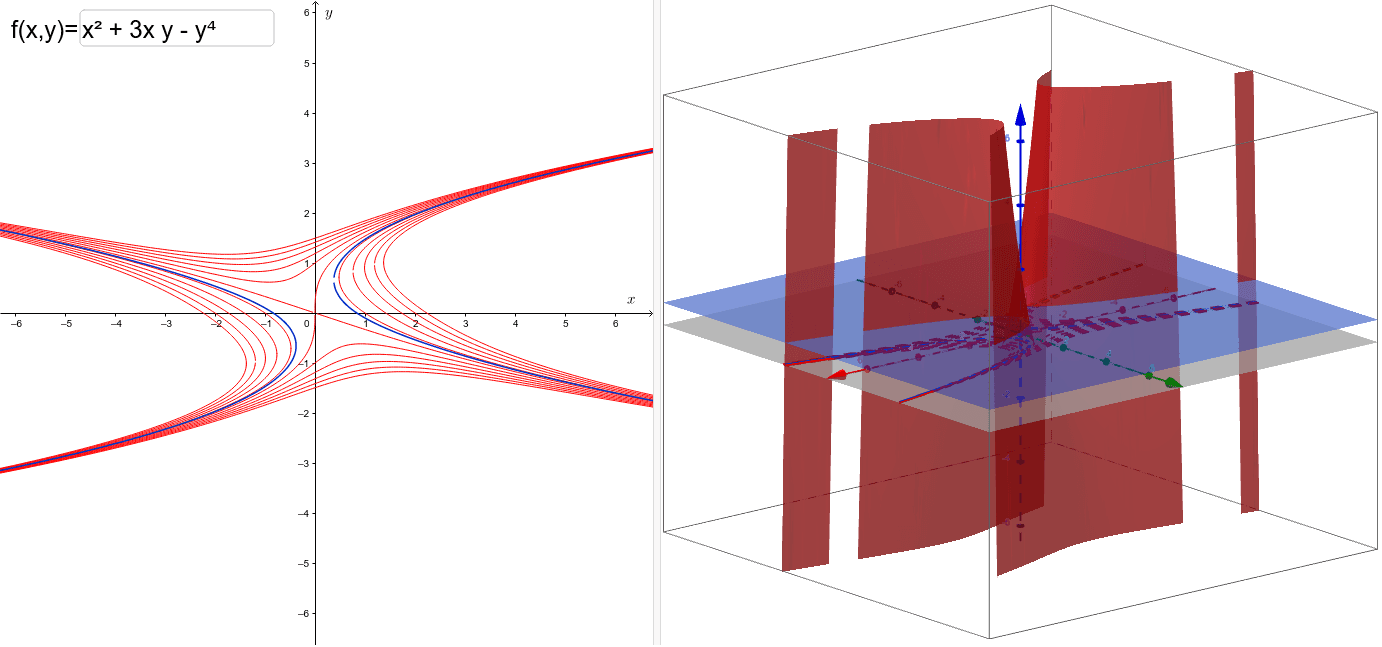



Level Curves Geogebra




Univ Vector Calculus Drawing A Contour Map With Level Curves Learnmath




Draw A Contour Map Of The Function Showing Several Level Curves F X Y Y 8x 2 Brainly Com




Contour Plots Video Khan Academy



Contour Lines Or Level Curves
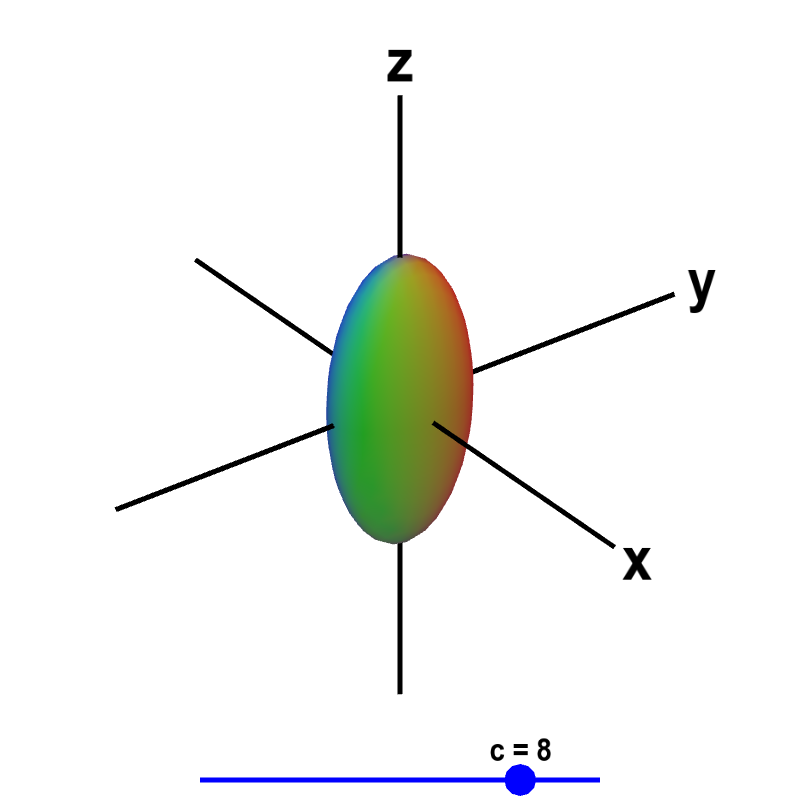



Level Sets Math Insight



Functions Of Several Variables Ximera



Contour Plots In Excel How To Create Contour Plots In Excel




Graph And Contour Plots Of Functions Of Two Variables Wolfram Demonstrations Project




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware



Level Curves Functions Of Several Variables By Openstax Page 3 12 Jobilize



Matplotlib Contour Plot



Contour Line Wikipedia



Level Curves And Contour Plots Mathonline



Level Curves And Contour Plots Mathonline




Draw A Contour Map Of The Function Showing Several Chegg Com




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware




Level Sets Math Insight




Calculus Iii Functions Of Several Variables




How To Read Contour Plot Mathematics Stack Exchange
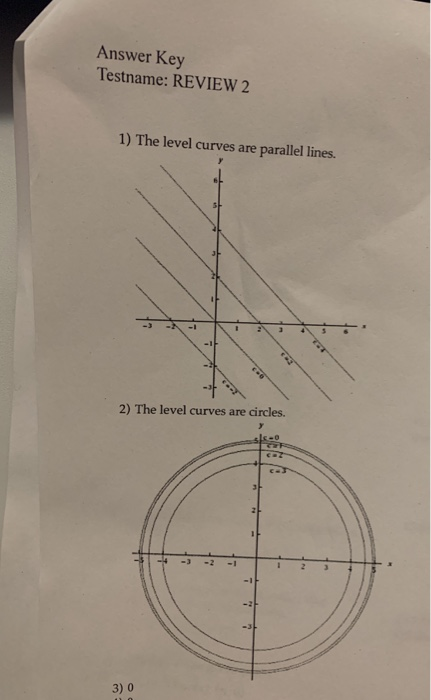



13 1 Describe The Level Curves Of The Function Chegg Com



Contour Lines Rodolphe Vaillant S Homepage
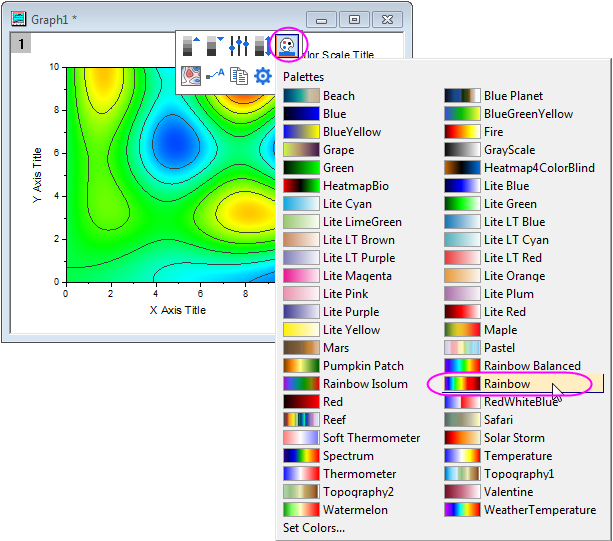



Help Online Tutorials Contour Plots And Color Mapping
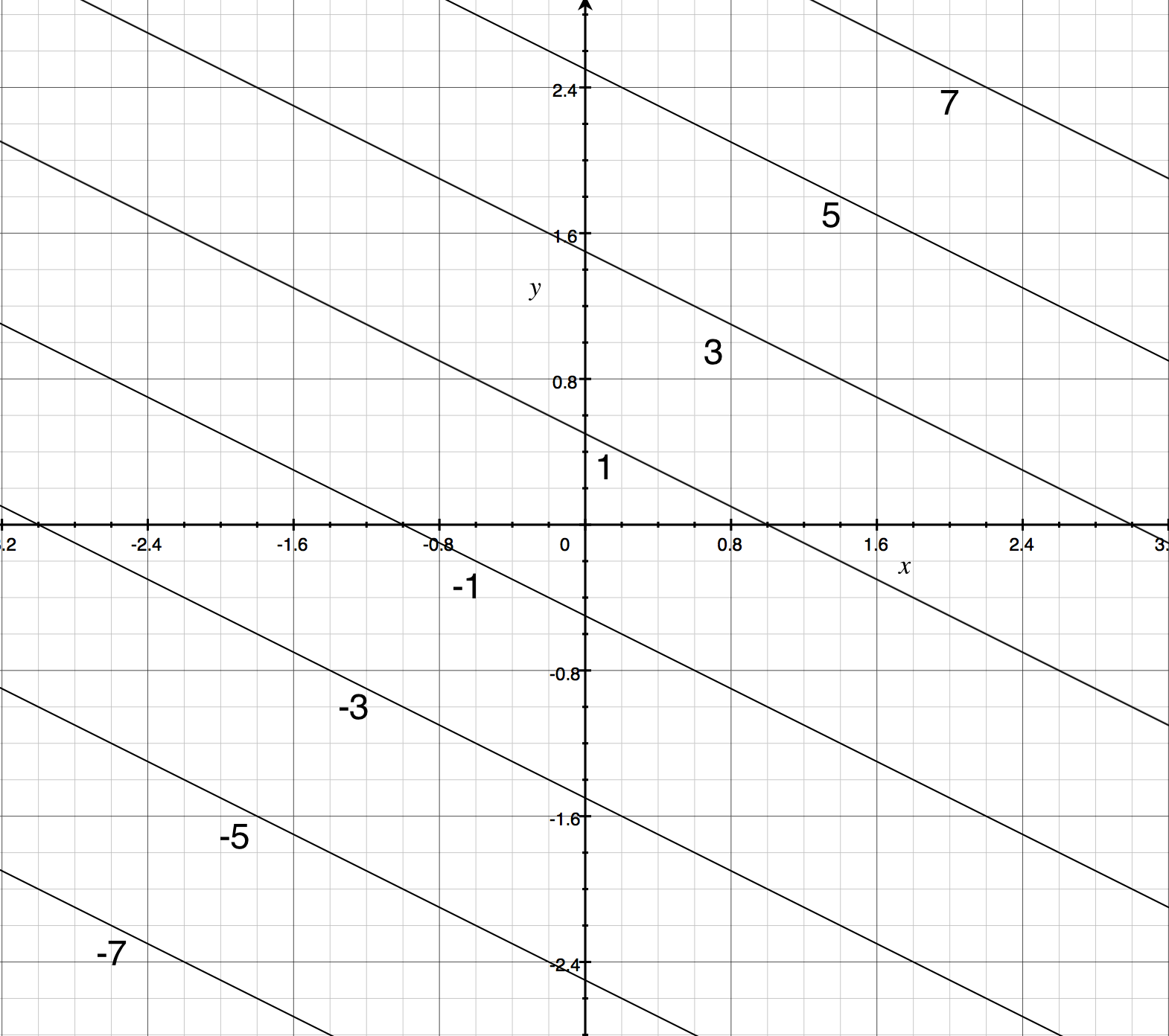



Contour Maps Article Khan Academy




Level Set Examples Math Insight




Level Curves And Contour Maps Calculus 3 Youtube



Http Academic Brcc Edu Ryanl Modules Multivariable Traces Traces Pdf




Which Linear Function Has The Contour Map That Is Shown Below With Level Curve C 0 As Indicated Assuming That The Contour Interval Is M 18 Study Com




Contour Plot An Overview Sciencedirect Topics



0 件のコメント:
コメントを投稿